- 热门产品:
品质保证
-
优秀销售团队提供7x24小时在线服务

-
质量稳定:实行全程过程监控全方位检测

-
价格合理:高效内部成本控制,让利于客户

-
交货快捷:采用先进生产工艺,缩短了交货期

您现在的位置:首页 > 工程案例
如何正确选用调节阀的流量特性?
发布于:2019/7/11 10:22:40 点击量:300
如何正确选用调节阀的流量特性?杜伯拉阀门技术君跟大家分享一下:
在过程控制系统的设计阶段,正确选用调节阀的流量特性(以下简称选用),是一个必须要解决的技术问题,对提高系统的调节品质起事半功倍的作用。
从现有文献看,理论选用方法尚在研究探索之中,设计中大都采用经验准则解决选用问题。然而各种文献给出的经验准则并非全都一致,有些经验准则对适用范围交待不清。例如常见的换热器出口温度控制系统,有相变传热与无相变传热的选用结论不全相同。若不明白选用理论,机械地套用经验准则,有可能会导致选用失误。因此,对选用的理论、及方法进行研究很有必要。
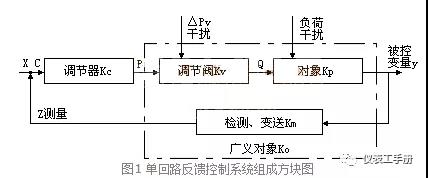
由图1可知,当调节器已整定,则Kc为常量,选用的理论依据为
Ko = Kv*Kp*Km≈常量 (1)
式中:Ko、Kv、Km—分别为系统广义对象、调节阀、被控对象、检测变送器的放大系数。
从选用角度分析式(1):
(1)选用的目的是以Kv补偿Kp、Km,对Ko作非线性校正。若系统运行中无干扰施入,即Kp、Km的工作点不变,则不需作非线性校正,选用任何一种流量特性调节阀都能符合式(1)要求。所以,无干扰就不存在选用问题,研究选用的理论与方法,必须联系干扰因素来了解其适用性。
(2)选用的过程是根据系统主要干扰作用下的Kp、Km变化规律,选定符合式(1)要求的,在该干扰作用下的Kv变化规律。由于Km的变化规律决定于检测、变送器整机输出入信号之间的固有函数关系,与干扰因素无关。因此,解决选用的关键,在于对系统主要干扰作用下的Kv、Kp变化规律的求取与了解。
(3)从现有的各种理论选用方法看,实质上都是采用定性分析的方法,来解决选用问题。所以对选用有实用意义的是了解常用的线性、对数,快开流量特性调节阀在各种干扰作用下所反映的Kv变化规律,以用作选用依据;了解常用的各种理论选用方法,求取干扰作用下Kp变化规律的可行性与适用性,这将对设计人员选择选用的方法,具有指导意义。
根据以上分析,文献通常给出的关于选用的论述,存在的问题主要表现为:对调节阀流量特性、Kv的论述,偏重一种形式,从选用角度看,有值得商榷之处;只给出理想工况(即阀前阀后压降ΔPv为恒值)下的各阀Kv变化规律,用于选用,对干扰的适用范围不清;没有联系干扰因素来论证求取Kv变化规律的可行性,以及对选用方法的适用性。因此,对选用缺乏实用意义,需加以修正与补充。
本文旨在解决上述问题,下文将探讨文献对阀流量特性、Kv的论述;从讨论阀流量特性与Kv的四种表达形式着手,以推导所得的用变量Q/Qmax、Q、C/Cmax或C所表征的各阀四种Kv表达式为依据,根据分析给出的有关变量在干扰作用下的状态,给出线性、对数、快开流量特性调节阀在干扰作用下所呈现的Kv变化规律,以及对选用的适用范围;论证求取干扰作用下Kp变化规律的可行性,及对选用方法的适用性。
2、探讨文献对阀流量特性、Kv的论述
2.1 分析有关变量在干扰作用下的状态
为方便下文的讨论,需先了解有关变量在干扰作用下的状态。某一开度或全开时阀的流量方程分别为:

式中:
g—重力加速度,是恒值;
ρ—密度,不可压缩流体p为恒值;
C—阀的流通能力;
Cmax—已确定通径调节阀的最大流通能力,实质上即为根据工艺参数计算所得的系统最大流量下的C值,在阀的标准产品系列中经设计人员合理圆整、选定的阀公称流通能力Cg,Cg为恒值,即Cmax为恒值。
无论用经验准则、或是理论方法选用,通常都是在众多干扰中,确定一个出现最频,对被控变量y影响最大的干扰,作为系统主要干扰变量来考虑选用,其它次要干扰则均视为常量。
干扰形式众多,一般可等效视为广义的负荷(即非Δpv干扰)或Δpv干扰两种类型。
由此,依据式(2)、(3)可知:
(1)定值系统负荷为主要干扰,Δpv等次要干扰可视为常量;Qmax为常量;Cmax为恒值;Q,C为变量。
(2)定值系统Δpv为主要干扰,负荷等次要干扰可视为常量;Δpv为变量;Cmax为恒值;由式(3)知,Qmax∝Δpv,即Qmax为变量;Q的状态可作如下分析,因给定值X为恒值,由工艺操作的物料或能量平衡原理,以及系统的调节过程可知,Δpv干扰施入之初引起Q的变化,会很快被系统的调节作用改变阀的开度所克服,系统稳态时Q仍为Δpv干扰施入前的流量值不变,所以Q仍可视为常量;C随阀的开度而变,所以C为变量。
以上结论,下文讨论中作为已知条件引用。
2.2、探讨文献通常采用的论述形式
对阀的流量特性,通常都以流体流过阀的相对流量Q/Qmax与阀杆相对行程L/Lmax之间的函数关系定义。
本文链接:http://www.kzpv.cn/projectcase/detail/20190711102240.html
